The ProofTools manual

Applicability

This manual applies to ProofTools versions 0.6.1 and earlier, however, features new from 0.6, including the small additions to its user interface - the ability to stipulate the number of rule applications to step by, and the progress window visible for longer, including infinite-branch, decompositions - have not yet been documented.

Otherwise, features not present in versions earlier than the latest are noted in yellow.

Table of contents

Introduction

ProofTools is a program that draws proof trees, either for their own sake or to check the validity of argument forms or the logical truth of formulas. Proof trees are also known as semantic trees, analytic tableau and semantic tableau. If you don't know what it means for an argument to be valid or for a formula to be logically true, if you don't know what propositional, predicate and modal logic are, if you don't recognise the logic symbols used in this manual, or if you don't know what a proof tree is, then you can read about these topics in the ProofTools background and technical addendum page.

Quickstart

Applicability note: status messages were not all as below in version 0.1 beta.

ProofTools can perform one of three functions. Choose which one you want to perform before continuing:

  1. Check whether an argument is valid.
  2. Check whether an individual formula is a logical truth.
  3. Simply draw a proof tree for a set of formulas, without trying to prove anything.

Perform the following steps depending on which function you wish to perform:

To check whether an argument is valid

  1. To start, open up ProofTools. If it is already open and the tree panel (#21) is not empty, then click the clear all button (#8).
  2. Enter the premises of the argument one at a time into the premise entry box (#16), pressing enter after each one.
  3. Enter the conclusion of the argument into the conclusion entry box (#18) and then press enter in that box.
  4. Click the show proof button (#11).

The proof tree will be drawn and the result will be shown in the status bar. Possible results are:

To check whether an individual formula is a logical truth

  1. To start, open up ProofTools. If it is already open and the tree panel (#21) is not empty, then click the clear all button (#8).
  2. Enter the individual formula into the conclusion entry box (#18) and then press enter in that box.
  3. Click the show proof button (#11).

The proof tree will be drawn and the result will be shown in the status bar. Possible results are:

To simply draw a proof tree for a set of formulas, without negating or trying to prove anything

  1. To start, open up ProofTools. If it is already open and the tree panel (#21) is not empty, then click the clear all button (#8).
  2. Enter the formulas in the set one at a time into the premise entry box (#16), pressing enter after each one.
  3. Click the show proof button (#11).

The proof tree will be drawn and the result will be shown in the status bar. Possible results are:

Interface elements

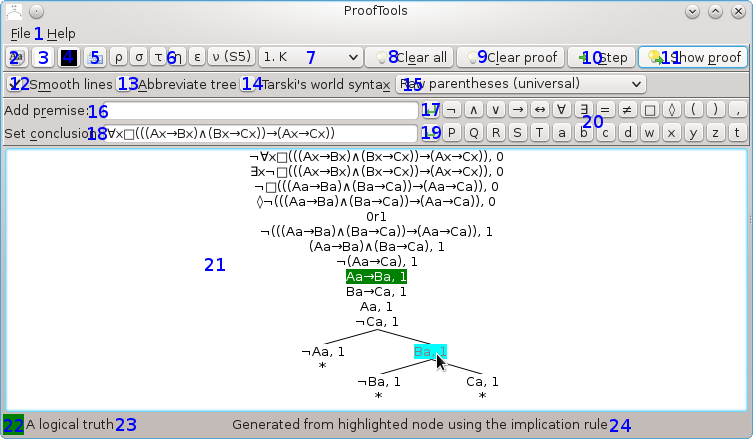
Annotated screenshot of the interface of ProofTools 0.5 beta
Figure 1: the ProofTools 0.5 beta interface with numbered elements
Main menu Font dialogue button Background colour button Foreground colour button Hotkey editor button Modal logic toggle buttons Modal logic dropdown box Clear all button Clear proof button Step button Show proof button Smooth lines checkbox Abbreviate tree checkbox Tarski's world syntax checkbox Parentheses (de)normalisation dropdown Premise entry box Premise entry button Conclusion entry box Conclusion entry button Logic symbols panel Tree panel Validation status icon Validation status text Message status text

  1. The sparse main menu contains "File" and "Help" sub-menus. Under "File" are the menu items "Export to image", "Run tests" and "Exit", which, respectively, export the proof tree to a PNG image, run a battery of tests, and close the program. Under "Help" are the menu items "Online manual", also accessible from anywhere in the program by pressing F1, which opens a web browser at this page, and "About", which displays authorship, version and changelog information about the program.

  2. Font dialogue button

    The font dialogue button, also accessible as ctrl+F, pops up a menu with the options to either set the interface font or to set the tree font. Clicking on either of those options will open up a font dialogue box from which the font for the interface or the tree can be set. The first time the dialogue box appears it might not contain the current font, however on subsequent appearances it will. The interface font is for everything aside from the main menu (#1), the status bar (#23 and #24), and the tree panel (#21). Because settings are currently not saved, the fonts will revert to default the next time the program is run.

  3. Background colour dialogue button

    The background colour dialogue button, also accessible as ctrl+B, is coloured the same as the current background colour of the tree panel. Clicking it opens a dialogue box that allows a new colour to be selected. The dialogue will open with its colour set to the current background colour. Because settings are currently not saved, the background colour will revert to default the next time the program runs.

  4. Foreground colour dialogue button

    The foreground colour dialogue button, also accessible as ctrl+L, is coloured the same as the current foreground colour of the tree panel. Clicking it opens a dialogue box that allows a new colour to be selected. The dialogue will open with its colour set to the current foreground colour. Because settings are currently not saved, the foreground colour will revert to default the next time the program runs.

  5. Hotkey editor button

    Applicability note: this button is not available in version 0.1 beta, and nor are logic symbol hotkeys.

    Tip: Symbol replacements, available since version 0.4 beta, might suit you better than hotkeys.

    The hotkey editor button, also accessible as ctrl+K, opens the hotkey editor in which the hotkeys for the logic symbols can be set:

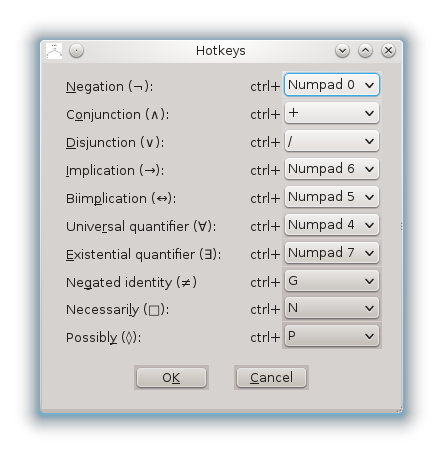
    Screenshot of the hotkeys editor in ProofTools 0.4 beta
    Figure 2: the ProofTools hotkeys editor

    A logic symbol hotkey is the combination of ctrl (as indicated in the dialogue) and the selected key. Missing from the drop-down menu selections are those hotkeys which are already assigned, those being ctrl+A for "select all", ctrl+B for the background colour dialogue, ctrl+C for "copy", ctrl+F for the font selection menu, ctrl+K for the hotkey editor, ctrl+L for the foreground colour dialogue, ctrl+V for "paste", ctrl+X for "cut", and, depending on the platform/widgetset, others.

    The editor does not check for duplicate hotkey assignments, so if the same key is assigned to two different symbols, then pressing it will insert the logic symbol for the first assigned symbol.

  6. Modal logic toggle buttons

    Applicability note: the Euclidean modal logic toggle button was added in version 0.5 beta. All other modal logic toggle buttons were added in version 0.4 beta.

    Any of the first five of these toggle buttons may be toggled on to enable, in combination with any of the others, a particular constraint on modal accessibility relations, leading to a variant of normal modal logic:

    • Reflexivity, ρ, corresponding to axiom T
    • Symmetry, σ, corresponding to axiom B
    • Transitivity, τ, corresponding to axiom 4
    • Extendability/seriality, η, corresponding to axiom D
    • Euclidean relations, ε, corresponding to axiom 5

    The sixth toggle button toggles the equivalence relation, ν, which implements modal logic S5, and which, if toggled on, toggles off all of the other toggles. Applicability note: prior to version 0.5 beta, toggling S5 on toggled the first three of the other toggles on and the last off, however, this was misleading because internally, distinct S5 rules (based on the equivalence relation) are implemented.

    Toggling any of these buttons will set the corresponding value of the modal logic dropdown box (#7).

    Modal semantics are as described below.

    If none of your input formulas (premises and/or conclusion) include either of the modal operators (□ and ◊), then these buttons have no effect.

  7. Modal logic dropdown box

    Applicability note: the modal logic dropdown box was added in version 0.5 beta.

    Any possible basic/normal modal logic variant can be selected via this dropdown box. Each variant is preceded by a number, and variants with the same number are logically equivalent (even though implemented with different accessibility relation rules). Selecting a variant with this dropdown box causes the appropriate modal logic toggle buttons (#6) to be toggled on/off.

    Modal semantics are as described below.

    If none of your input formulas (premises and/or conclusion) include either of the modal operators (□ and ◊), then this dropdown box has no effect.

  8. Clear all button

    The clear all button clears all nodes from the proof tree, including the initial premises and the negated conclusion. It is also accessible as alt+E.

  9. Clear proof button

    The clear proof button clears only the proof nodes from the proof tree, leaving the initial premises and the conclusion intact. It is also accessible as alt+L.

  10. Step button

    The step button applies the next rule to the proof tree. If that rule is the final rule, then after the rule has been applied the status of the validation is displayed in the status bar. A notification message is popped up if neither a premise nor a conclusion have been set, or if the tree has already had all rules applied to it. This button is also accessible as alt+S.

    Applicability note: in version 0.1 beta it was mandatory for a conclusion to have been set prior to clicking this button.

  11. Show proof button

    The show proof button applies all rules to the proof tree in one operation, and shows the result of the validation in the status bar. A notification message is popped up if neither a premise nor a conclusion have been set, or if the tree has already had all rules applied to it. It is also accessible as alt+P.

    Applicability note: in version 0.1 beta it was mandatory for a conclusion to have been set prior to clicking this button.

  12. Smooth lines checkbox

    When the smooth lines checkbox is checked, lines in the proof tree will be drawn smoothly by the ProofTools code, i.e. with antialiasing enabled. When unchecked, the ProofTools code will not draw lines smoothly, however on some operating systems they may be drawn smoothly anyway.

  13. Abbreviate tree checkbox

    Applicability note: abbreviated trees were introduced in version 0.4 beta, where they could not be toggled, and were in constant effect. The user-interface toggle for this feature was introduced in version 0.4.2 beta.

    Checking this box has the effect of potentially reducing the size of trees. This is achieved as follows:

    To avoid redundant nodes, ProofTools does not apply rules to a branch where to do so would add to the branch only nodes that already exist on it, or that will be a subset of the result of a prior pending rule application. The only exception is that ProofTools will still apply the rule when the only place in which the nodes that the rule would add exist is a prior pending rule application that splits the branch (this exception exists primarily because it simplifies the code).

    So, if "Abbreviate tree" is enabled, and you're wondering why a node isn't being broken down, then ask yourself which node(s) it would be broken down into, and scan up the branch and check whether (all of) those/that node(s) already exist on it, or whether any of the previous nodes on the branch would break down, without splitting, into either the same (set of) node(s), or into a superset of it/them. If either of these checks turn out to be true, then you've found the reason why ProofTools isn't breaking down the node.

  14. Tarski's world syntax checkbox

    Applicability note: the Tarski's world syntax checkbox was added in version 0.4 beta.

    Checking this box changes the expected syntax and the way it is parsed, from default syntax to Tarski's world syntax. The differences between default syntax and Tarski's world syntax are as described below.

  15. Parentheses (de)normalisation dropdown

    Applicability note: the parentheses (de)normalisation dropdown was added in version 0.4.2 beta.

    This dropdown stipulates how ProofTools will display parentheses in tree nodes. There are two primary options: "raw" parentheses and "normalised" parentheses. When "raw" parentheses are selected, then parentheses are displayed as entered by the user as far as this is possible. When "normalised" parentheses are selected, then parentheses are displayed as minimally as necessary to show syntactical groups and precedences in each formula as entered by the user.

    For an example of what this means in practice, if the "raw" parentheses form of a formula is (((◊∀xPx∨Qx∧¬(Rx)))), then this will be normalised as ◊(∀x)(Px∨(Qx∧(¬Rx)))

    .

    Each primary option has a secondary option: to apply the choice to the entire tree or only to nodes added from that point onwards.

  16. Premise entry box

    Applicability note: logic symbol hotkeys are not available in version 0.1 beta.

    The premise entry box accepts the keyboard entry of a well-formed formula. If the premise entry box is currently active or was the last active text box, then clicking any of the logic symbol buttons in the logic symbols panel (#6) or using either of the logic symbol keyboard shortcut methods will insert the respective logic symbol into the premise entry box at the cursor.

    Upon pressing enter or clicking the premise entry button (#16) to the right, the formula will be parsed and, if well-formed, added as a node on the initial branch of the proof tree. Any existing part of the proof tree below the premises and the (optional) negated conclusion will be deleted because changing the premises and/or conclusion changes the tree. If the formula is not well-formed, then a parse error message will be displayed explaining why.

    Pressing alt+R places the edit focus into the premise entry box.

  17. Premise entry button

    Clicking the premise entry button performs the same function as pressing enter in the premise entry box (#16).

  18. Conclusion entry box

    Applicability note: logic symbol hotkeys are not available in version 0.1 beta.

    The conclusion entry box accepts the keyboard entry of a well-formed formula. If the conclusion entry box is currently active or was the last active text box, then clicking any of the logic symbol buttons in the logic symbols panel (#6) or using either of the logic symbol keyboard shortcut methods will insert the respective logic symbol into the conclusion entry box at the cursor.

    Upon pressing enter or clicking the conclusion entry button (#19) to the right, the formula will be parsed and, if well-formed, negated and set as the conclusion node on the initial branch of the proof tree, replacing any existing negated-conclusion node. Any existing proof tree below the conclusion will be deleted because changing the conclusion changes the tree. If the formula is not well-formed, then a parse error message will be displayed explaining why.

    Pressing alt+C places the edit focus into the conclusion entry box.

  19. Conclusion entry button

    Clicking the conclusion entry button performs the same function as pressing enter in the conclusion entry box (#18).

  20. Logic symbols panel

    Applicability note: logic symbol hotkeys are not available in version 0.1 beta, and nor are predicate logic symbols: predicate logic was not supported in version 0.1 beta.

    Clicking on any of the logic symbols in the logic symbols panel will insert the button's symbol into the last active text box (either the premise entry box (#16) or the conclusion entry box (#18)) at its current cursor location. Each button without a corresponding key on the keyboard has a keyboard shortcut.

  21. Tree panel

    The proof tree is drawn in the tree panel. The font, background colour and foreground colour of this panel can all be set: see the font dialogue button (#2), the background colour dialogue button (#3) and the foreground colour dialogue button (#4).

  22. Validation status icon

    Applicability note: this status icon was not present in version 0.1 beta.

    The colour of the validation status icon indicates the current validation status of the tree. It complements the validation status text. The colours have the following meanings:

    The same colour as the status bar's background
    The proof has not been started yet.
    Yellow
    The proof is in progress, due to either a click on the Step or the Show proof buttons.
    Green
    The proof is complete and all branches closed; if both conclusion and premises are set this means that the argument is valid, if only the conclusion is set this means that the conclusion is a logical truth, otherwise it simply means that the tree is closed.
    Red
    The proof is complete and not all branches closed; this can occur when running out of constants (applicability note: since version 0.4 beta, ProofTools will never run out of constants), but otherwise it means that if both conclusion and premises are set then the argument is invalid, and if only the conclusion is set then the conclusion is not a logical truth, and otherwise simply that the tree is unclosed.

  23. Validation status text

    Applicability note: in version 0.1 beta this text status was combined with the message status text (#24) and featured slightly different messages. As well, infinite branch messages never occurred in version 0.1 because it supported only propositional logic in which infinite branches are impossible.

    The validation status text describes the current validation status of the tree. It complements the validation status icon. The possible values and their meanings are:

    Ready
    The proof has not been started yet.
    In progress
    The proof is in progress, due to a click on either of the Step or the Show proof buttons.
    All closed
    The proof is complete, all branches closed (applies when a conclusion has not been set).
    Not all closed
    The proof is complete, not all branches closed, (applies when a conclusion has not been set).
    Not all closed (∞ tree) (in version 0.2 beta the infinity symbol was instead a word, "infinite")
    The proof is complete, but the tree is infinite and not all branches closed (applies when a conclusion has not been set).
    Valid argument
    The proof is complete and all branches closed (applies when a conclusion and (in version 0.2.1 beta and above) at least one premise were set). If premises were also set then this indicates that the entire argument is valid; (what follows applies to version 0.2 beta only) if no premises were set then it indicates that the conclusion is a logical truth.
    Invalid argument
    The proof is complete and not all branches closed (applies when a conclusion and at least one premise were set). If premises were also set then this indicates that the entire argument is invalid, (what follows applies to version 0.2 beta only) if no premises were set then it indicates that the conclusion is not a logical truth.
    Invalid argument (∞ tree) (in version 0.2 beta the infinity symbol was instead a word, "infinite")
    The proof is complete, but the tree is infinite and not all branches closed (applies when a conclusion and at least one premise were set). If premises were also set then this indicates that the entire argument is invalid, (what follows applies to version 0.2 beta only) if no premises were set then it indicates that the conclusion is not a logical truth.
    A logical truth
    The proof is complete and all branches closed (applies when a conclusion only was set). This indicates that the formula entered into the conclusion entry box is a logical truth.
    NOT a logical truth
    The proof is complete and not all branches closed (applies when a conclusion only was set). This indicates that the formula entered into the conclusion entry box is not a logical truth.
    NOT a logical truth (∞ tree)
    The proof is complete, but the tree is infinite and not all branches closed (applies when a conclusion only was set). This indicates that the formula entered into the conclusion entry box is not a logical truth.
    Ran out of constants
    The tree was so large that there weren't enough constants to finish constructing it (applicability note: since version 0.4 beta, ProofTools will never run out of constants).

  24. Message status text

    Applicability note: in version 0.1 beta this text status is combined with the validation status text (#23) and features slightly different messages. Several messages, too, have been added in version 0.4 beta.

    Note to self: need to review these subsequent to the 0.5 beta release.

    The message status text shows the result of operations. The various possible messages in alphabetical order and when/why they occur are:

    Antialiasing enabled / Antialiasing disabled
    Shown immediately after the smooth lines checkbox (#12) is checked/unchecked (respectively).
    Changed background colour
    Shown immediately after the background colour dialogue button (#3) is pressed and a colour selected.
    Conclusion set
    Shown immediately after the conclusion is successfully set or changed by pressing the conclusion entry button (#19), or by pressing enter in the conclusion entry box (#18).
    Enabled S5 / Disabled S5
    Shown immediately after the S5 toggle button (#6) is checked/unchecked (respectively).
    Generated from highlighted ... [Mouse-over messages]
    When hovering the mouse cursor over a node in the tree, these display the rule used to generate the node as well as the node/s from which it was generated.
    Parse error whilst adding premise
    Shown when a premise is submitted and it is not well-formed. At the same time a message box appears with details of the parse error.
    Parse error whilst setting conclusion
    Shown when the conclusion is submitted by pressing the conclusion entry button (#19), or by pressing enter in the conclusion entry box (#18), and the conclusion is not well-formed. At the same time, a message box appears with details of the parse error.
    Premise added
    Shown immediately after a premise is successfully added to the tree by pressing the premise entry button (#17), or by pressing enter in the premise entry box (#16).
    Proof deleted
    Shown after the proof is deleted by clicking the clear proof button (#9).
    Ran tests
    Shown immediately after the tests window is closed.
    Set interface font
    Shown immediately after the interface font is set by clicking on the font dialogue button (#2) or pressing ctrl+F, selecting "Set interface font", and choosing a new font through the dialogue that appears.
    Set tree font
    Shown immediately after the tree font is set by clicking on the font dialogue button (#2) or pressing ctrl+F, selecting "Set tree font", and choosing a new font through the dialogue that appears.
    Stepped once
    Shown immediately after the Step button is clicked and a single rule is applied but there are still more rules to be applied (otherwise one of the "Validation complete" messages is shown).
    Tarski's world syntax enabled / Tarski's world syntax disabled
    Shown immediately after the Tarski's world syntax checkbox (#14) is checked/unchecked (respectively).
    Tree deleted
    Shown after the entire proof tree is successfully deleted by clicking on the clear all button (#8).
    Turned modal [reflexivity/symmetry/transitivity/extendability] [on/off]
    Shown immediately after the modal reflexivity (ρ) toggle button / modal symmetry (σ) toggle button / modal transitivity (τ) toggle button / modal extendability (η) toggle button (respectively) is toggled on/off (respectively). In conjunction with the S5 toggle button, these buttons make up the modal toggle buttons (#6).
    Validation complete
    Shown immediately after either all rules have been applied to the tree or the program runs out of constants, but only when a conclusion has been set.
    Validation complete. Warning: no conclusion set - this is NOT a proof.
    Shown immediately after all rules have been applied to the tree, but only when no conclusion has been set,. The warning indicates that no negation has been applied to any of the formulae that the tree was drawn for, so that it does not indicate the truth or validity of any of the premises as entered; it can, however, be considered as a test of whether the negation of the conjunction of the premises is a logical truth: if all branches close then that test has succeeded.

Interface features

Logic symbol keyboard shortcuts and hotkeys

Applicability note: symbol replacements were added in version 0.4 beta. Hotkeys are not available in version 0.1 beta.

Standard keyboards do not by default provide a straightforward way to generate most of the logic symbols that ProofTools recognises in its premise and conclusion entry boxes. ProofTools thus provides convenience methods to generate them through the keyboard, so as to avoid the otherwise cumbersome method of clicking the logic symbol buttons.

The original, and still available, method that ProofTools provides is hotkeys of the form ctrl+hotkey, where hotkey is an assigned keyboard character. Default hotkeys are provided that can be changed through the hotkey editor, accessible via the hotkey editor button (#5). Certain characters are unavailable as ctrl shortcuts, and one problem with this method is that, with ProofTools being a cross-platform tool, the set of such characters varies from platform to platform, making consistent defaults impossible, at least if they are to be mnemonic.

The new method is symbol replacements. Thus, if, for example, "->" is typed into one of the formula entry boxes, it is replaced on-the-fly with "→". This applies also to text copy-and-pasted into the entry boxes: all possible symbol replacements are applied to the pasted text, including those formed when the pasted characters combine with pre-existing characters in the entry box to form a symbol replacement. All possible symbol replacements are as follows, with accompanying mnemonics:

DescriptionTypeReplaced withMnemonic
Less-than sign, hyphen (aka minus sign), greater-than sign<->↔Visual correspondence
Backslash, hyphen (aka minus sign), forward slash\-/∀Visual correspondence
Backslash, forward slash\/∨
Applicability note: in version 0.4 beta, this replacement symbol was ∀		Visual correspondence
Pipe aka vertical line|∨Corresponds in the C programming language with the "bitwise or" operator, a semantic relation to logical disjunction. Non-programmers might instead like to associate this through thinking of it as a vertical border separating two areas, so that the area to the left can be chosen or the area to the right.
Hyphen (aka minus sign), greater-than sign->→Visual correspondence
Open square bracket, close square bracket[]□Visual correspondence
Less-than sign, greater-than sign<>◊Visual correspondence
Forward slash, equals sign/=≠Visual correspondence
Exclamation mark (aka bang)!¬Corresponds with the negation operator in programming languages such as C, PHP and Javascript. Non-programmers might instead like to associate this through its use as a punctuation mark of emphasis in written language - an emphasis on the contrary: "Something is WRONG!" i.e. "The OPPOSITE is true!" i.e. "Negate this!"
Hyphen (aka minus sign), pipe aka vertical line-|¬Visual correspondence (somewhat)
Applicability note: added in version 0.4.2
Forward slash, backslash/\∧Visual correspondence
Applicability note: added in version 0.4.2
Ampersand&∧Semantic correspondence (an ampersand stands in for "and", which semantically is conjunction). It also corresponds in the C programming language with the "bitwise and" operator, a close semantic relation to logical conjunction.
Close square bracket]∃Visual correspondence
Hyphen (aka minus sign), close square bracket-]∃Visual correspondence
Applicability note: added in version 0.4.2

Tracing rules by hovering the mouse pointer over nodes

To find out which rule generated a node, and which node/s that rule was applied to to generate it, simply hover the mouse pointer over the node. This will highlight the node itself by colouring it aqua, will colour the primary node to which a rule was applied to generate the mouse-over node green, and will colour any secondary node (e.g. the node containing the constant in a universal quantifier rule application) used to generate the mouse-over node lime. It will also change the message status text (#24) to indicate the rule that was used to generate the node, including which variable was replaced by which constant in the case of certain predicate logic rules.

Copying trees, nodes and counter-models via right-click context menus

To copy the entire tree to the clipboard as a PNG image, simply right-click anywhere in the tree panel (#21) and select "Copy tree as image". To copy the text of a node to the clipboard, simply right-click on the node and select "Copy node formula". To copy the text of a counter-model to the clipboard, simply right-click on the counter-model popup and select "Copy counter-model". Counter-models are copied as both plain text and rich text format, so that if you paste into a word processor, subscripts will be formatted (but only to the first level of subscripting - rich text format doesn't support the formatting of second-level subscripts, which are used in some counter-models).

Counter-model popups

If a branch does not close, i.e. it does not terminate in an asterisk, then a counter-model can be constructed out of it. This applies to both ordinary open branches (those terminating in "o") and infinite open branches (those terminating in "∞"). If the mouse is hovered over either the "o" or the "∞", a window will pop up containing the counter-model. Counter-models are formed as described in the reference text, in particular in sections:

Accepted syntax

Default syntax versus Tarski's world syntax

Applicability note: Tarski's world syntax was added in version 0.4 beta.

Two basic syntaxes are supported: default syntax and Tarski's world syntax. Tarski's world syntax was added by request, and can be enabled via its checkbox. What follows describes the default syntax; the ways in which Tarski's world syntax varies from default syntax are described afterwards.

Propositional logic

Applicability notes: modifying propositions with digits is only supported from version 0.4 beta onwards.

ProofTools supports the following propositional logic operators. For their logical semantics (which are standard), including truth tables, please see the Propositional logic operators section of the ProofTools background and technical addendum page.

SymbolMeaningNumber of operands
¬NegationOne (following the operator)
∧ConjunctionTwo (one on either side of the operator)
∨DisjunctionTwo (one on either side of the operator)
→Material conditionalTwo (one on either side of the operator)
↔Material equivalenceTwo (one on either side of the operator)

Propositions are represented by uppercase letters A to Z, optionally followed immediately by any number of digits (there may not be whitespace between the letter and the digits or between any of the digits).

Parentheses are optional, and, if omitted, are implied by operator precedence. Operator precedence from highest to lowest is: negation, conjunction, disjunction, material conditional, then material equivalence. Thus, the following well-formed formula:

¬A∧B∨C→D↔E

is parsed as:

((((¬A)∧B)∨C)→D)↔E

and its reverse:

A↔B→C∨D∧¬E

is parsed as:

A↔(B→(C∨(D∧(¬E))))

Operators of the same type are parsed left-to-right, so that for example A→B→C is parsed as (A→B)→C. For all operators other than the material conditional, this is the same as right-to-left parsing, as demonstrated in the Left-to-right parsing versus right-to-left parsing section of the ProofTools background and technical addendum page.

Other examples:

Formation rules for propositional logic are given in the ProofTools background and technical addendum page.

Predicate logic

Applicability notes: predicate logic is not supported in version 0.1 beta, and the modification of predicate names, constants and variables with digits, as well as the identity and negated identity operators, is only supported from version 0.4 beta onwards.

Predicate logic operators are as for propositional logic, with the addition of the following four operators: the universal quantifier, ∀, the existential quantifier (also called the particular quantifier), ∃, the identity operator, =, and the negated identity operator, ≠. For the logical semantics of these four operators (which are standard), please see the Quantification operators (∀ and ∃) and Identity (=) and negated identity (≠) sections of the ProofTools background and technical addendum page.

The two predicate logic operators must each be followed by a single variable, represented by a lowercase character from w to z, plus t, optionally followed immediately by any number of digits (there may not be whitespace between the letter and the digits or between any of the digits). They then quantify one or more predicates over that variable. A predicate is represented by a predicate name followed by one or more constants or variables. A predicate name is a capital letter, optionally followed immediately by any number of digits (there may not be whitespace between the letter and the digits or between any of the digits). A constant is represented by a lowercase character from a to v, minus t, optionally followed immediately by any number of digits (there may not be whitespace between the letter and the digits or between any of the digits). One simplest example of a well-formed predicate logic formula is Pa; two simplest examples of well-formed predicate logic formulas including quantifiers are ∀xPx and ∃xPx. Another example of a simple predicate logic formula is ∀xPxabc.

Quantifiers can be parenthesised, as, for example, (∀x)Px or (∀x)(Pxabc) (the latter style of parenthesising is the standard syntax). As for propositional logic, any pair of parentheses can be nested to any depth and the extraneous parentheses are ignored, so that ((((∀x))))(((Px))) gets parsed simply as (∀x)(Pxabc). Quantifiers can also be nested, with or without parentheses, such that ∀x∃yPxy, (∀x)(∃y)(Pxy) and (∀x)((∃y)(Pxy)) are equivalent.

As for propositional logic, all parentheses can be omitted, in which case implicit parentheses will be added during parsing. The additional parsing rules for predicate logic are that quantifiers are "minimally greedy": their scope will be extended as far as is necessary to capture the maximum number of predicates containing the quantified variable, but no further. This means that, for example, in the unparenthesised example, ∀xPx∨Qc↔R→Sx∧T, the implicit parentheses will be parsed as such: ((∀x)(Px∨Qc↔R→Sx))∧T. In this example, the maximum number of predicates containing the variable x is reached with the inclusion of Sx, and so the scope of the implicit parentheses ends there.

Predicate logic formulas that are not well formed include:

Quantifiers can be nested to any depth, and needn't be nested immediately subsequent to a prior quantifier, so that, for example, the following formula is well formed:

∀xPx∧∃yQy→∀zRxyz

and is parsed with implicit parentheses as follows:

(∀x)(Px∧(∃y)(Qy→(∀z)(Rxyz)))

Modal logic

Applicability note: modal logic was added in version 0.4 beta.

Modal logic operators are as for predicate logic, with the addition of the following two operators: the necessity operator, □, and the possibility operator, ◊. These operators function syntactically identically with the negation operator, ¬, i.e. they have highest precedence and bind to the expression immediately to their right. (Negated) identity expressions are treated in their entirety when modal operators are applied to them, such that □a=b is parsed as □(a=b).

Whitespace

Applicability note: in version 0.1 beta, any whitespace generates a parse error.

Whitespace is insignificant, except within names for propositions, predicates, variables and constants, within which it may not occur. Whitespace characters are: space, tab, carriage return and linefeed. So, for example, the formula " ( (∀ x1 ) ¬ ( P x1 c d ) ) ∧ Q " is parsed as ((∀x1)(¬Px1cd))∧Q

Tarski's world syntax

Tarski's world syntax differs from default syntax only in these ways:

Tarski's world predicate names

The predicate names valid in Tarski's world syntax, along with the number of variables/constants they take, are as follows:

Predicate nameNumber of variables/constants
Tet1
Cube1
Dodec1
Small1
Large1
Medium1
LeftOf2
RightOf2
BackOf2
FrontOf2
Adjoins2
Smaller2
Larger2
SameRow2
SameCol2
SameSize2
SameShape2
Between3

Parse error messages

If a formula entered through either of the premise or conclusion text entry boxes is not well formed (not syntactically valid), then one of the following error messages will be raised (this hopefully is a complete list, but I can't guarantee that I haven't missed any). In what follows:

Applicability note: in versions prior to 0.4 beta, there are no quotes around {character}. Additionally, some of these error messages do not occur in versions prior to 0.4 beta: to avoid excessive and distracting annotations, those messages are not marked.

Note to self: need to review the code to ensure that this list is complete and correct.

A note on adjustment of messages for Tarski's world syntax: some messages below refer to a valid range of letters for constants and/or variables. These ranges are as in the default syntax. When Tarski's world syntax is enabled, ProofTools adjusts these ranges in such messages such that the range appropriate to Tarski's world syntax is shown.

Error: the quantifier whose opening declaration ends at character {number} does not range over any variable.
This error is described above.
Phrase is empty.
The entered formula contains nothing, possibly except for whitespace.
Error at character {number}: expected an uppercase character A through Z, or a constant (a lowercase character a through v, minus t) or any variable under quantification, or one of ¬, ∀, ∃, □, ◊ or an opening parenthesis; instead got "{character}". Applicability note: in versions prior to 0.4 beta, the text "or a constant (a lowercase character a through v, minus t) or any variable under quantification, " and "□, ◊ " is not present.
This error occurs when on the right side of an operator but before the end of the formula, an appropriate character - the start of a predicate/proposition/variable/constant, or a unary operator, or an opening parenthesis - is not found.
Error: unexpected end of line; was expecting an uppercase character A through Z, or a constant (a lowercase character a through v, minus t) or any variable under quantification, or one of ¬, ∀, ∃, □, ◊ or an opening parenthesis. Applicability note: as above.
As for the above error except that it is raised when the operator occurs at the end of a formula.
Error: the quantifier using variable {variable} at position {number} falls within the scope of the earlier quantifier using the same variable and whose scope starts at position {number}.
This error is described above.
Error at character {number}: expected a variable (a lowercase character w through z, plus t); instead got "{character}".
This error occurs when a quantifier (∀ or ∃) is not followed by a variable, but is instead followed by some other character. It complements the error message below.
Error: unexpected end of line; was expecting a variable (a lowercase character w through z, plus t).
As above except that it occurs when a quantifier occurs at the end of the formula.
Error: free (unquantified) variable at character {number}.
This error is described above.
Error: the predicate {capital letter} is defined at character {number} to take {number} variable/s but it is also defined at character {number} to take a different number, {number} of variables.
This error is described above.
Error: unexpected closing parenthesis at character {number} - no matching opening parenthesis found.
Self-explanatory.
Error: unexpected end of line: missing one or more closing parentheses. In versions prior to 0.4 beta, the text "one or more closing parentheses" instead read "a closing parenthesis".
Self-explanatory.
[It looks like you are trying to use Tarski's world syntax, which is currently turned off - do you need to turn it on? The parse error is: ]Error at character {number}: expected [[a lowercase character a through z,|= or ≠,|a binary operator other than = or ≠,]] [[or a closing parenthesis| or the end of the expression]]; instead got {character}.
This error occurs after a predicate/proposition/variable/constant, when the next appropriate symbol (generally a binary operator) is not found. What the next appropriate symbol actually is though depends on context, which is why the message contains optional and variant parts. The first part, asking whether to turn on Tarski's world syntax, occurs when an opening parenthesis is detected after a string of symbols that look like a predicate name - this is invalid in default syntax but valid in Tarski's world syntax, so the parser prompts you to turn on Tarski's world syntax if indeed that is what you want. The text, "a lowercase character a through z", is shown when default syntax is enabled and the text at the location prior to that of this error is or could be a predicate (i.e. it is either a capital letter or a capital letter followed by a string of lowercase letters, each optionally followed by a string of digits). In this case a binary operator is not the only choice; equally valid is for the predicate to be continued. The text, "= or ≠,", is shown when the text at the location prior to that of this error is an isolated (i.e. not part of a predicate) variable or constant, such that only identity or negated identity is valid next. In contrast, the text, "a binary operator other than = or ≠," is shown when the text at the location prior to that of this error is not an isolated (i.e. not part of a predicate) variable or constant, such that any other binary operator is valid next. The text "or a closing parenthesis" is shown when parentheses are open and it is valid to close them where the error occurred. If, instead, parentheses are not open, and it is valid to end the expression (i.e. an identity or negated identity operator is not expected), then the text " or the end of the expression" is shown.
Error at character {number}: digits are not permitted after variables using the letter "{character}".
This error occurs only when Tarski's world syntax is turned on, and a variable is modified by appending digits to it: digits are not permitted in variables in Tarski's world syntax.
Error at character {number}: digits are not permitted after constants using the letter "{character}".
This error occurs only when Tarski's world syntax is turned on, and a constant is modified by appending digits to it: digits are not permitted in constants in Tarski's world syntax other than for constants beginning with "n", in which case digits are required.
Error at character {number}: digits are required after constants using the letter "n".
This error occurs only when Tarski's world syntax is turned on, and a constant beginning with "n" is not modified by appending digits to it: digits are not permitted in constants in Tarski's world syntax other than for constants beginning with "n", in which case digits are required.
Error at character {number}: expected an opening parenthesis; instead got "{character}".
This error occurs only when Tarski's world syntax is turned on, when a predicate name is not followed by an open parenthesis (after which its variables/constants should appear, separated by commas - these don't affect the error, however, and I include this extra parenthesised comment for information only). This error complements the error below.
Error: unexpected end of line; was expecting an opening parenthesis.
As above except that it occurs when the end of line rather than some other character is encountered.
Error at character {number}: expected a comma; instead got "{character}".
This error occurs only when Tarski's world syntax is turned on, and when a predicate name that takes multiple constants/variables does not contain enough comma-separated such constants/variables. For example, the Tarski's world predicate, "Smaller", takes two constants/variables, so a valid occurrence of it is Smaller(a,b). This error would occur if only one constant was supplied, as in Smaller(a). The comma is expected for the second constant/variable where the closing parenthesis is.
Error: unexpected end of line; was expecting a comma.
As above except that it occurs when the end of line rather than some other character (such as a closing parenthesis, as in the example above), is encountered.
Error: unknown (assumed-to-be-predicate) name, "{string}" at position {number}.
This error only occurs when Tarski's world syntax is turned on, and when a predicate name is used that does not match any of the predicate names valid in that syntax.
Error at character {number}: expected an opening parenthesis or a constant (a lowercase character a through v, minus t) or any variable under quantification; instead got "{character}".
This error occurs when a constant or variable, optionally enclosed in any number of pairs of parentheses, does not occur after an identity (=) or negated identity (≠) symbol.
Error: unexpected end of line; was expecting an opening parenthesis or a constant (a lowercase character a through v, minus t) or any variable under quantification.
As above but where the end of formula occurs rather than some other invalid character.
Error: modal operator "[[□|◊]]" found at position {number}, however modal operators are not supported by Tarski's world syntax.
This error only occurs when Tarski's world syntax is turned on, and when a modal operator is encountered: as the message explains, modal operators are not supported when Tarski's world syntax is enabled.
Error at character {number}: expected a variable; instead got the constant "{string}".
This error occurs when a quantification operator (∀ or ∃) is followed by a letter valid as constant (optionally modified by digits if Tarski's world syntax is not enabled or if the letter is "n") rather than a letter valid as a variable (also optionally modified by digits if Tarski's world syntax is not enabled). Letters valid as constants and variables are listed in the Predicate logic and Tarski's world syntax sections above.
Error at character {character}: expected = or ≠,; instead got "{character}".
This error occurs when, in a place where an identity would be syntactically valid, a variable/constant occurs on its own and not as part of an identity (i.e. not followed by either = or ≠).
Error: the formula terminated in a bare constant that was not a part of an identity (=) or negated identity (≠). This is not permitted.
This error complements the error above: a bare constant (i.e. one not part of a predicate) may only appear as part of an identity or negated identity expression: this error is shown when a bare constant occurs at the end of the entered formula i.e. one that is not part of an identity or negated identity expression.

Modal semantics

Applicability note: initial modal logic features were added in version 0.4 beta. The Euclidean accessibility relation and the modal logic dropdown box were added in version 0.5 beta.

ProofTools supports all basic/normal modal logics. Basic/normal modal logic variants can be set using the modal toggle buttons or the modal logic dropdown box in the toolbar, changes to each of which are reflected in the other.

When combining modal operators with predicate logic operators, modal semantics are constant domain and contingent identity. A future version of ProofTools may support variable domain and necessary identity too.

Other features

Infinite branch detection and handling

Applicability note: Infinite branch detection has been disabled from version 0.6 aside from straightforward detection of infinite branches due to application of the modal extensibility rule. This is because the algorithm was flawed and gave the wrong results in some cases.

Applicability note: This feature does not apply to version 0.1 beta, in which infinite loops cannot occur because it supports only propositional logic.

The proof tree rules for predicate and modal logic can sometimes result in infinite branches. The simplest case in which this occurs for predicate logic is when any node consists of a formula of the form ∀x∃yPxy. Various (but not all) combinations of modal characteristics can result in infinite trees when a node consists of certain formulas, the simplest case form of such a formula in S5 modal logic is ◊□◊P.

In versions prior to 0.6, ProofTools tried to detect and avoid infinite branches in trees containing predicate and modal logic operators. We had intended that if it was possible to close a branch, ProofTools would do it, regardless of whether that branch could otherwise become infinite. We intended, in other words, that ProofTools would not allow infinite branches to prevent a tree that could be closed from closing. We also intended that if, however, a branch was infinite and it could not be closed, then ProofTools would indicate this with an infinity symbol (∞) at the bottom of the branch.

We got this wrong. The bug is described in the update of 2019-02-09.

Known bugs and limitations

See the known bugs and limitations section of the main page.